U metodi nejednakosti, želimo ograničiti broj mogućnosti tako da najprije ograničimo neku nepoznanicu pomoću nejednakosti. Zatim nam ostaje relativno malo primjera koje možemo provjeriti ručno i vidjeti ima li rješenja.
PRIMJER:
U skupu prirodnih brojeva riješite jednadžbu 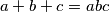 .
.
RJEŠENJE:
Pošto je jednadžba potpuno simetrična, bez smanjenja općenitosti neka je 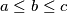 . Tada je
. Tada je 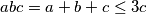 , odnosno
, odnosno 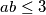 (kako je
(kako je 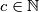 , smijemo nejednakost podijeliti s
, smijemo nejednakost podijeliti s  ) , pa razlikujemo tri slučaja:
) , pa razlikujemo tri slučaja:  Dakle, jedino rješenje je
Dakle, jedino rješenje je 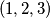 i sve permutacije tog skupa.
i sve permutacije tog skupa.
PRIMJER:
Dokažite da izraz 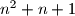 , gdje je
, gdje je  , ne može biti kvadrat cijelog broja.
, ne može biti kvadrat cijelog broja.
RJEŠENJE:
Metoda koju ćemo primijeniti poznata je i kao smještanje među kvadrate, tj. pokazujemo da broj ne može biti kvadrat tako da ga smjestimo između dva uzastopna kvadrata.
Primijetimo da zbog  tj.
tj. 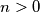 vrijedi
vrijedi 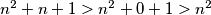 . S druge strane, slično zaključujemo i
. S druge strane, slično zaključujemo i 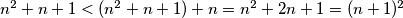 . No kako su
. No kako su  i
i  su 2 uzastopna prirodna broja, a
su 2 uzastopna prirodna broja, a  strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
Zadatci za samostalno rješavanje
1. (Općinsko 2010. SŠ4 4.) Odredi sve parove prirodnih brojeva 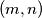 takvih da vrijedi
takvih da vrijedi 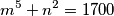 .
.
2. (Županijsko 2018. SŠ1 2.) Odredi sve parove cijelih brojeva 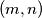 takve da je:
takve da je: 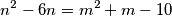
U metodi nejednakosti, želimo ograničiti broj mogućnosti tako da najprije ograničimo neku nepoznanicu pomoću nejednakosti. Zatim nam ostaje relativno malo primjera koje možemo provjeriti ručno i vidjeti ima li rješenja.
PRIMJER:
U skupu prirodnih brojeva riješite jednadžbu $a + b + c = abc$.
RJEŠENJE:
Pošto je jednadžba potpuno simetrična, bez smanjenja općenitosti neka je $a \leq b \leq c$. Tada je $abc = a + b + c \leq 3c$, odnosno $ab \leq 3$ (kako je $c \in \mathbb{N}$, smijemo nejednakost podijeliti s $c$) , pa razlikujemo tri slučaja:
\begin{enumerate}
\item $a = 1, b = 1$ (uvrštavanjem te vrijednosti u početnu jednadžbu dobijemo kontradikciju $2 = 0$);
\item $a = 1, b = 2$ (dobivamo $c = 3$);
\item $a = 1, b = 3$ (dobivamo $c = 2$ što je kontradikcija s $b \leq c$).
\end{enumerate}
Dakle, jedino rješenje je $(1, 2, 3)$ i sve permutacije tog skupa.
PRIMJER:
Dokažite da izraz $n^2 + n + 1$, gdje je $n \in \mathbb{N}$, ne može biti kvadrat cijelog broja.
RJEŠENJE:
Metoda koju ćemo primijeniti poznata je i kao \textbf{smještanje među kvadrate}, tj. pokazujemo da broj ne može biti kvadrat tako da ga smjestimo između dva uzastopna kvadrata.
Primijetimo da zbog $n \in \mathbb{N}$ tj. $n > 0$ vrijedi $n^2 + n + 1 > n^2 + 0 + 1 > n^2$. S druge strane, slično zaključujemo i $n^2 + n + 1 < (n^2 + n + 1) + n = n^2 + 2n + 1 = (n + 1)^2$. No kako su $n$ i $n + 1$ su 2 uzastopna prirodna broja, a $n^2 + n + 1$ strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
\textbf{Zadatci za samostalno rješavanje}
1. (Općinsko 2010. SŠ4 4.) Odredi sve parove prirodnih brojeva $(m,n)$ takvih da vrijedi $$m^5+n^2=1700$$.
2. (Županijsko 2018. SŠ1 2.) Odredi sve parove cijelih brojeva $(m,n)$ takve da je: $$n^2 - 6n = m^2 + m - 10$$
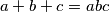 .
.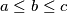 . Tada je
. Tada je 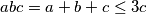 , odnosno
, odnosno 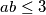 (kako je
(kako je 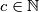 , smijemo nejednakost podijeliti s
, smijemo nejednakost podijeliti s  ) , pa razlikujemo tri slučaja:
) , pa razlikujemo tri slučaja:  Dakle, jedino rješenje je
Dakle, jedino rješenje je 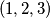 i sve permutacije tog skupa.
i sve permutacije tog skupa.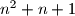 , gdje je
, gdje je  , ne može biti kvadrat cijelog broja.
, ne može biti kvadrat cijelog broja. tj.
tj. 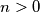 vrijedi
vrijedi 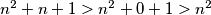 . S druge strane, slično zaključujemo i
. S druge strane, slično zaključujemo i 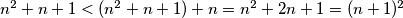 . No kako su
. No kako su  i
i 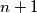 su 2 uzastopna prirodna broja, a
su 2 uzastopna prirodna broja, a 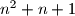 strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.
strogo između njihovih kvadrata, taj broj nikako ne može biti kvadrat nekog prirodnog broj.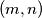 takvih da vrijedi
takvih da vrijedi 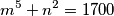 .
.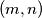 takve da je:
takve da je: 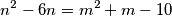
 Školjka
Školjka 
