Djeljivost (Uvod)
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Djeljivost je jedan od najosnovnijih, ali i najvažnijih pojmova u teoriji brojeva. Za brojeve 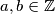 ,
, 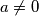 , kažemo da
, kažemo da  dijeli
dijeli  i pišemo
i pišemo 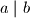 ako postoji cijeli broj
ako postoji cijeli broj  takav da je
takav da je 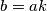 . Kažemo da je
. Kažemo da je  djelitelj od
djelitelj od  , odnosno da je
, odnosno da je  višekratnik od
višekratnik od  .
.
Prisjetimo se i osnovnih pravila djeljivosti:

Teorem od dijeljenju s ostatkom: Za proizvoljan prirodan broj  i cijeli broj
i cijeli broj  postoje jedinstveni cijeli brojevi
postoje jedinstveni cijeli brojevi  i
i  takvi da je
takvi da je 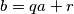 ,
, 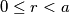 .
.
 Školjka
Školjka 
