\textbf{Djeljivost} je jedan od najosnovnijih, ali i najvažnijih pojmova u teoriji brojeva. Za brojeve $a, b \in \mathbb{Z}$, $a \neq 0$, kažemo da $a$ \textit{dijeli} $b$ i pišemo $a\mid b$ ako postoji cijeli broj $k$ takav da je $b=ak$. Kažemo da je $a$ \textit{djelitelj} od $b$, odnosno da je $b$ \textit{višekratnik} od $a$.
Prisjetimo se i osnovnih pravila djeljivosti:
\begin{itemize}
\item Broj je djeljiv s $2$ ako mu je zadnja znamenka djeljiva s $2$.
\item Broj je djeljiv s $3$ ako mu je zadnja zbroj znamenaka djeljiv s $3$.
\item Broj je djeljiv s $4$ ako su mu posljednje dvije znamenke djeljive s $4$.
\item Broj je djeljiv s $5$ ako mu je zadnja znamenka djeljiva s $5$.
\item Broj je djeljiv s $8$ ako su mu posljednje tri znamenke djeljive s $8$.
\item Broj je djeljiv s $9$ ako mu je zbroj znamenaka djeljiv s $9$.
\end{itemize}
\textbf{Teorem od dijeljenju s ostatkom:} Za proizvoljan prirodan broj $a$ i cijeli broj $b$ postoje jedinstveni cijeli brojevi $q$ i $r$ takvi da je $b=qa+r$, $0\leq r <a$.
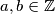 ,
, 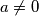 , kažemo da
, kažemo da  dijeli
dijeli  i pišemo
i pišemo 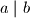 ako postoji cijeli broj
ako postoji cijeli broj  takav da je
takav da je 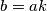 . Kažemo da je
. Kažemo da je  djelitelj od
djelitelj od  , odnosno da je
, odnosno da je  višekratnik od
višekratnik od  .
.
 i cijeli broj
i cijeli broj  postoje jedinstveni cijeli brojevi
postoje jedinstveni cijeli brojevi  i
i  takvi da je
takvi da je 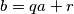 ,
, 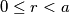 .
.  Školjka
Školjka