Princip matematičke indukcije moćan je i elegantan alat za dokazivanje tvrdnji 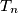 koje ovise o
koje ovise o  za sve prirodne brojeve
za sve prirodne brojeve 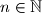 . Kod dokazivanja matematičkom indukcijom uz pretpostavku da željena tvrdnja vrijedi za neki proizvoljan prirodan broj
. Kod dokazivanja matematičkom indukcijom uz pretpostavku da željena tvrdnja vrijedi za neki proizvoljan prirodan broj  pokazujemo da tada nužno vrijedi tvrdnja i za
pokazujemo da tada nužno vrijedi tvrdnja i za  . Ono što nam nedostaje je provjera da za neki prirodan broj tvrdnja stvarno vrijedi (ne pretpostavljamo, nego izravno dokazujemo da vrijedi).
. Ono što nam nedostaje je provjera da za neki prirodan broj tvrdnja stvarno vrijedi (ne pretpostavljamo, nego izravno dokazujemo da vrijedi).
Formalno, matematička indukcija sastavljena je od  dijela:
dijela: 
Indukciju možemo vizualizirati dominama - najprije moramo srušiti prvu dominu u nizu, a zatim znamo da će ona srušiti sljedeću, koja će srušiti sljedeću, koja će srušiti sljedeću... i tako će na kraju srušiti sve domine, tj. tvrdnju ćemo pokazati za sve prirodne brojeve.
Ne smijemo zaboraviti provjeriti vrijedi li baza indukcije! Beskorisno nam je da svaka domina koja se ruši uzrokuje rušenje sljedeće ako nismo uspjeli srušiti prvu.
Osim na skupu prirodnih brojeva indukciju možemo koristiti na konačnim i prebrojivo beskonačnim skupovima (npr. parni prirodni brojevi, cijeli brojevi, prirodni brojevi veći od  , prosti brojevi), a to će nekada dovesti i do modifikacije baze i/ili koraka indukcije.
, prosti brojevi), a to će nekada dovesti i do modifikacije baze i/ili koraka indukcije.
Princip matematičke indukcije moćan je i elegantan alat za dokazivanje tvrdnji $T_n$ koje ovise o $n$ za sve prirodne brojeve $n\in \mathbb{N}$. Kod dokazivanja matematičkom indukcijom uz pretpostavku da željena tvrdnja vrijedi za neki proizvoljan prirodan broj $k$ pokazujemo da tada nužno vrijedi tvrdnja i za $k+1$. Ono što nam nedostaje je provjera da za neki prirodan broj tvrdnja stvarno vrijedi (ne pretpostavljamo, nego izravno dokazujemo da vrijedi).
Formalno, matematička indukcija sastavljena je od $3$ dijela:
\begin{enumerate}
\item \textbf{baza} ($T_1$): pokažemo da tvrdnja vrijedi za $n=1$ ili neki drugi "najmanji slučaj".
\item \textbf{pretpostavka} ($T_k$): pretpostavimo da vrijedi tvrdnja za neki $k \in \mathbb{N}$
\item \textbf{korak indukcije} ($T_{k+1}$): koristeći pretpostavku pokazujemo da tvrdnja vrijedi i za $k+1$
\end{enumerate}
Indukciju možemo vizualizirati dominama - najprije moramo srušiti prvu dominu u nizu, a zatim znamo da će ona srušiti sljedeću, koja će srušiti sljedeću, koja će srušiti sljedeću... i tako će na kraju srušiti sve domine, tj. tvrdnju ćemo pokazati za sve prirodne brojeve.
\textbf{Ne smijemo zaboraviti provjeriti vrijedi li baza indukcije!} Beskorisno nam je da svaka domina koja se ruši uzrokuje rušenje sljedeće ako nismo uspjeli srušiti prvu.
Osim na skupu prirodnih brojeva indukciju možemo koristiti na konačnim i prebrojivo beskonačnim skupovima (npr. parni prirodni brojevi, cijeli brojevi, prirodni brojevi veći od $3$, prosti brojevi), a to će nekada dovesti i do modifikacije baze i/ili koraka indukcije.
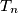 koje ovise o
koje ovise o  za sve prirodne brojeve
za sve prirodne brojeve 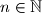 . Kod dokazivanja matematičkom indukcijom uz pretpostavku da željena tvrdnja vrijedi za neki proizvoljan prirodan broj
. Kod dokazivanja matematičkom indukcijom uz pretpostavku da željena tvrdnja vrijedi za neki proizvoljan prirodan broj  pokazujemo da tada nužno vrijedi tvrdnja i za
pokazujemo da tada nužno vrijedi tvrdnja i za  . Ono što nam nedostaje je provjera da za neki prirodan broj tvrdnja stvarno vrijedi (ne pretpostavljamo, nego izravno dokazujemo da vrijedi).
. Ono što nam nedostaje je provjera da za neki prirodan broj tvrdnja stvarno vrijedi (ne pretpostavljamo, nego izravno dokazujemo da vrijedi). dijela:
dijela: 
 , prosti brojevi), a to će nekada dovesti i do modifikacije baze i/ili koraka indukcije.
, prosti brojevi), a to će nekada dovesti i do modifikacije baze i/ili koraka indukcije.  Školjka
Školjka 
