ZADATAK: \textit{(Gaussova dosjetka)} Neka je $n \in \mathbb{N}$. Dokaži: $1+2+ \dots + n = \dfrac{n(n+1)}{2}$.
RJEŠENJE: Tvrdnju ćemo dokazati koristeći matematičku indukciju.
\begin{itemize}
\item [\textbf{B:}] Provjeravamo tvrdnju za $n=1$. Očito je $1 = \frac{1\cdot 2}{2}$ pa smo pokazali bazu indukcije.
\item[\textbf{P:}] Pretpostavimo sada da za neki prirodan broj $k\in\mathbb N$ vrijedi $1+2+...+k = \frac{k\cdot (k+1)}{2}$.
\item[\textbf{K:}] Želimo koristeći pretpostavku za $k$ pokazati da je $1+2+\dots+k+k+1 = \frac{(k+1)\cdot (k+2)}{2}$
\end{itemize}
Želimo pokazati da tvrdnja vrijedi i za $k+1$. Zato uzimamo pretpostavku i dodajemo joj $k+1$:
\begin{align*}
1+2+...+k &= \frac{k\cdot (k+1)}{2}\qquad\Big/+(k+1)\\
1+2+...+k+(k+1) &= \frac{k\cdot (k+1)}{2}+k+1\\
1+2+...+k+(k+1) &= \frac{k\cdot (k+1)+2(k+1)}{2}\\
1+2+...+k+(k+1) &= \frac{(k+2)\cdot (k+1)}{2}
\end{align*}
Time smo dokazali korak indukcije pa po principu matematičke indukcije zaključujemo da tvrdnja vrijedi za sve prirodne brojeve $n$.
 . Dokaži:
. Dokaži: 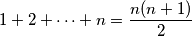 .
.![\begin{itemize}
\item [\textbf{B:}] Provjeravamo tvrdnju za $n=1$. Očito je $1 = \frac{1\cdot 2}{2}$ pa smo pokazali bazu indukcije.
\item[\textbf{P:}] Pretpostavimo sada da za neki prirodan broj $k\in\mathbb N$ vrijedi $1+2+...+k = \frac{k\cdot (k+1)}{2}$.
\item[\textbf{K:}] Želimo koristeći pretpostavku za $k$ pokazati da je $1+2+\dots+k+k+1 = \frac{(k+1)\cdot (k+2)}{2}$
\end{itemize}](/media/m/3/f/1/3f179f1d0e826bef4611a71a795a306b.png) Želimo pokazati da tvrdnja vrijedi i za
Želimo pokazati da tvrdnja vrijedi i za  . Zato uzimamo pretpostavku i dodajemo joj
. Zato uzimamo pretpostavku i dodajemo joj  :
: 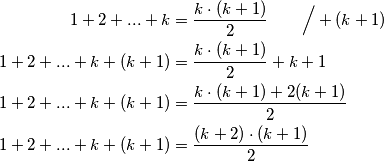 Time smo dokazali korak indukcije pa po principu matematičke indukcije zaključujemo da tvrdnja vrijedi za sve prirodne brojeve
Time smo dokazali korak indukcije pa po principu matematičke indukcije zaključujemo da tvrdnja vrijedi za sve prirodne brojeve  .
.  Školjka
Školjka 
