U konveksnom četverokutu

točke
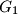
,
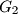
,
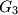
,
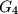
su redom težišta trokuta
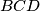
,

,

,

, dok su

,

,

,
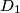
, točke centralno simetrične točkama

,

,

,

u odnosu na
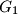
,
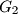
,
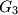
,
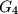
. Dokažite da je

paralelogram ako i samo ako je
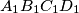
paralelogram.
%V0
U konveksnom četverokutu $ABCD$ točke $G_1$, $G_2$, $G_3$, $G_4$ su redom težišta trokuta $BCD$, $ACD$, $ABD$, $ABC$, dok su $A_1$, $B_1$, $C_1$, $D_1$, točke centralno simetrične točkama $A$, $B$, $C$, $D$ u odnosu na $G_1$, $G_2$, $G_3$, $G_4$. Dokažite da je $ABCD$ paralelogram ako i samo ako je $A_1B_1C_1D_1$ paralelogram.