Na strani

trostrane piramide

dana je točka

, kroz koju su povučene dužine
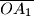
,
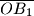
i
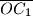
, paralelno s bridovima
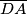
,
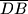
i
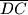
, do presjeka

,

,

sa stranama piramide. Dokažite da je
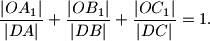
%V0
Na strani $ABC$ trostrane piramide $ABCD$ dana je točka $O$, kroz koju su povučene dužine $\overline{OA_1}$, $\overline{OB_1}$ i $\overline{OC_1}$, paralelno s bridovima $\overline{DA}$, $\overline{DB}$ i $\overline{DC}$, do presjeka $A_1$, $B_1$, $C_1$ sa stranama piramide. Dokažite da je $$
\dfrac{|OA_1|}{|DA|}+\dfrac{|OB_1|}{|DB|}+\dfrac{|OC_1|}{|DC|}=1.
$$