U ravnini su dane točke

,

i

. Neka su

,

,

,

,

i

točke u istoj ravnini takve da su trokuti

,
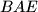
,
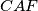
,
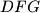
,
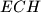
i
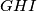
pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka

polovište dužine
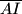
.
%V0
U ravnini su dane točke $A$, $B$ i $C$. Neka su $D$, $E$, $F$, $G$, $H$ i $I$ točke u istoj ravnini takve da su trokuti $ABD$, $BAE$, $CAF$, $DFG$, $ECH$ i $GHI$ pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka $E$ polovište dužine $\overline{AI}$.