U Sunčevom sustavu otkriven je novi planet! Dakle, oko Sunca kruži  planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše
planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše  planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
 planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše
planeta. Dokaži da se u svakom trenutku na površini Sunca može pronaći točka iz koje su vidljiva najviše  planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.)
planeta. (Općepoznata pretpostavka je da svi planeti i Sunce imaju oblik kugle te da svaki planet ima manji polumjer od Sunca. Druga saznanja o planetama molimo ne koristiti.) Slični zadaci
Zadan je jednakostraničan trokut. Dozvoljeni potez je da pravcem presiječemo trenutni lik na dva dijela, "okrenemo" jedan od nastalih dijelova i ponovo ”zalijepimo”. (npr. ako to napravimo po visini jednakostraničnog trokuta stranice  , dobit ćemo paralelogram stranica
, dobit ćemo paralelogram stranica 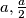 i kutom od
i kutom od 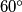 ) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
 , dobit ćemo paralelogram stranica
, dobit ćemo paralelogram stranica 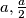 i kutom od
i kutom od 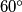 ) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!
) Možemo li nizom takvih poteza iz trokuta dobiti kvadrat? Ako da - pokaži kako, ako ne - dokaži!  Školjka
Školjka  trokuta
trokuta  leže redom točke
leže redom točke  ,
,  i
i  , pri čemu je
, pri čemu je 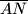 visina,
visina, 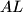 simetrala kuta
simetrala kuta 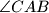 i
i 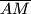 težišnica. Ako je
težišnica. Ako je 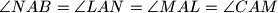 , odredite kutove trokuta.
, odredite kutove trokuta.  i
i  kutova
kutova  (
( i
i  su točke na stranicama
su točke na stranicama  ). Nađite kut
). Nađite kut 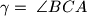 ako je
ako je 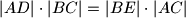 i
i 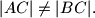
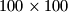 upisani su brojevi
upisani su brojevi 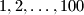 i to tako da se svaki pojavljuje točno
i to tako da se svaki pojavljuje točno  puta. Pokažite da postoji redak ili stupac u kojem ima barem
puta. Pokažite da postoji redak ili stupac u kojem ima barem  iz unutrašnjosti ili s ruba trokuta
iz unutrašnjosti ili s ruba trokuta 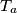 ,
, 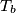 ,
, 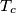 su redom nožišta okomica iz
su redom nožišta okomica iz  ,
,  . Ako je
. Ako je 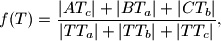 dokažite da
dokažite da 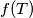 ne ovisi o izboru točke
ne ovisi o izboru točke