Trokut

je šiljastokutan. Za bilo koju točku

iz unutrašnjosti ili s ruba trokuta

, točke
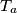
,
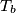
,
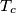
su redom nožišta okomica iz

na stranice

,

,

. Ako je
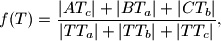
dokažite da
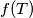
ne ovisi o izboru točke

ako i samo ako je trokut

jednakostraničan.
%V0
Trokut $ABC$ je šiljastokutan. Za bilo koju točku $T$ iz unutrašnjosti ili s ruba trokuta $ABC$, točke $T_a$, $T_b$, $T_c$ su redom nožišta okomica iz $T$ na stranice $\overline{BC}$, $\overline{CA}$, $\overline{AB}$. Ako je $$
f(T)=\dfrac{|AT_c|+|BT_a|+|CT_b|}{|TT_a|+|TT_b|+|TT_c|},
$$ dokažite da $f(T)$ ne ovisi o izboru točke $T$ ako i samo ako je trokut $ABC$ jednakostraničan.