Neka je
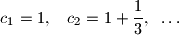
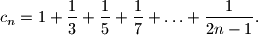
Dokažite da vrijedi
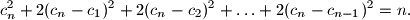
%V0
Neka je $$
c_1 = 1,\;\;\;c_2 = 1 + \frac{1}{3},\;\;\ldots
$$ $$
c_n = 1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \ldots +
\frac{1}{2n - 1}.
$$ Dokažite da vrijedi $$
c_n^2 + 2(c_n - c_1)^2 + 2(c_n - c_2)^2 + \ldots + 2(c_n - c_{n-1})^2 = n.
$$