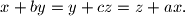Slični zadaci
Na šahovskom turniru s osam sudionika svaka dvojica odigrala su po jednu partiju. Nakon odigrane partije pobjednik dobiva  bod, a poraženi
bod, a poraženi  bodova. Ako partija završi remisom svaki od njih dobiva po
bodova. Ako partija završi remisom svaki od njih dobiva po  boda. Na kraju turnira svaka dva sudionika imaju različit broj bodova, a drugoplasirani šahist ima toliko bodova koliko ih imaju posljednja četvorica zajedno. Koliko je bodova osvojio sedmoplasirani igrač u partiji s trećeplasiranim?
boda. Na kraju turnira svaka dva sudionika imaju različit broj bodova, a drugoplasirani šahist ima toliko bodova koliko ih imaju posljednja četvorica zajedno. Koliko je bodova osvojio sedmoplasirani igrač u partiji s trećeplasiranim?
 bod, a poraženi
bod, a poraženi  bodova. Ako partija završi remisom svaki od njih dobiva po
bodova. Ako partija završi remisom svaki od njih dobiva po  boda. Na kraju turnira svaka dva sudionika imaju različit broj bodova, a drugoplasirani šahist ima toliko bodova koliko ih imaju posljednja četvorica zajedno. Koliko je bodova osvojio sedmoplasirani igrač u partiji s trećeplasiranim?
boda. Na kraju turnira svaka dva sudionika imaju različit broj bodova, a drugoplasirani šahist ima toliko bodova koliko ih imaju posljednja četvorica zajedno. Koliko je bodova osvojio sedmoplasirani igrač u partiji s trećeplasiranim?  Školjka
Školjka  Dokažite da se vrhovi
Dokažite da se vrhovi 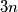 -terostrane prizme mogu obojati s tri boje na takav način da svaki vrh bude spojen bridovima s vrhovima svih triju boja.
-terostrane prizme mogu obojati s tri boje na takav način da svaki vrh bude spojen bridovima s vrhovima svih triju boja. Dokažite da ako se vrhovi
Dokažite da ako se vrhovi  -terostrane prizme mogu obojati s tri boje tako da je svaki vrh spojen bridovima s vrhovima svih triju boja, onda je
-terostrane prizme mogu obojati s tri boje tako da je svaki vrh spojen bridovima s vrhovima svih triju boja, onda je  .
.  ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše
ispunjena je jedinicama i nulama. Poznate je da ne postoje četiri jedinice na mjestima koje čine pravokutnik. Dokažite da je broj jedinica u tablici najviše 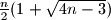 .
. 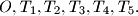 Dokazi da postoje indeksi
Dokazi da postoje indeksi 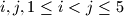 takvi da je
takvi da je 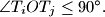
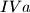 ,
, 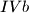 ,
, 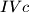 ,
, 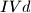 ,
, 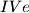 i
i 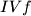 trebaju ići na maturalno putovanje, a moguća odredišta su Kopački rit, Plitvička jezera, Trakošćan i Kornati. Na koliko načina oni to mogu učiniti, ako svaki razred može otići na samo jedno od tih mjesta, a svako od njih mora posjetiti barem jedan razred?
trebaju ići na maturalno putovanje, a moguća odredišta su Kopački rit, Plitvička jezera, Trakošćan i Kornati. Na koliko načina oni to mogu učiniti, ako svaki razred može otići na samo jedno od tih mjesta, a svako od njih mora posjetiti barem jedan razred?  ,
,  ,
,  ako uz zadane brojeve
ako uz zadane brojeve  ,
,  ,
,  ,
, 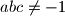 , vrijede jednakosti
, vrijede jednakosti