Za realan broj

definiraju se: najveće cijelo od

,
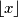
je najveći cijeli broj koji nije veći od

i decimalni dio od

,
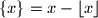
.
Npr.
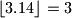
,
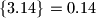
,
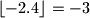
,
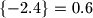
.
Odredi sve pozitivne brojeve

za kojeg su
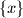
,
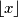
i

tri uzastopna člana geometrijskog niza.
%V0
Za realan broj $x$ definiraju se: najveće cijelo od $x$, $\lfloor x \rfloor$ je najveći cijeli broj koji nije veći od $x$ i decimalni dio od $x$, $\{x\}=x-\lfloor x\rfloor$.
Npr.\ $\lfloor 3.14\rfloor =3$, $\{3.14\}=0.14$, $\lfloor -2.4 \rfloor =-3$, $\{-2.4\}=0.6$.
Odredi sve pozitivne brojeve $x$ za kojeg su $\{x\}$, $\lfloor x \rfloor $ i $x$ tri uzastopna člana geometrijskog niza.