Slični zadaci
Kružnice  i
i  , polumjera
, polumjera  i
i  redom (
redom (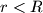 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.
 i
i  , polumjera
, polumjera  i
i  redom (
redom (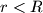 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  pravac paralelan njihovoj zajedničkoj tangenti, neka je
pravac paralelan njihovoj zajedničkoj tangenti, neka je  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , a
, a  jedno sjecište pravca
jedno sjecište pravca  s kružnicom
s kružnicom  , tako da se točke
, tako da se točke  i
i  nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu
nalaze s iste strane pravca koji spaja središta danih kružnica. Dokaži da polumjer kružnice opisane trokutu  ne ovisi o izboru pravca
ne ovisi o izboru pravca  i izrazi taj polumjer pomoću
i izrazi taj polumjer pomoću  i
i  .
.  Školjka
Školjka  točka na stranici
točka na stranici  danog šiljastokutnog trokuta
danog šiljastokutnog trokuta  i
i  središta kružnica opisanih trokutima
središta kružnica opisanih trokutima 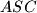 i
i 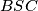 . Odredite položaj točke
. Odredite položaj točke 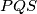 ima najmanju moguću površinu.
ima najmanju moguću površinu.  ,
,  ,
,  ,
,  ,
,  i
i  točke u istoj ravnini takve da su trokuti
točke u istoj ravnini takve da su trokuti  ,
, 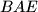 ,
, 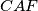 ,
, 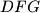 ,
, 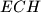 i
i 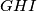 pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka
pozitivno orijentirani jednakostranični trokuti. Dokažite da je točka 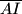 .
. 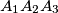 označimo:
označimo: 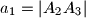 ,
, 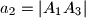 ,
, 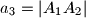 . Duljine visina tog trokuta iz vrhova
. Duljine visina tog trokuta iz vrhova  ,
, 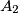 ,
, 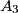 označimo redom sa
označimo redom sa 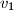 ,
, 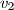 ,
, 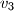 . Promatrajmo sve brojeve oblika
. Promatrajmo sve brojeve oblika 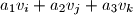 gdje je
gdje je 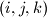 bilo koja permutacija skupa
bilo koja permutacija skupa 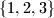 . Nađite najmanji od tih brojeva i izrazite ga pomoću površine
. Nađite najmanji od tih brojeva i izrazite ga pomoću površine  iz unutrašnjosti ili s ruba trokuta
iz unutrašnjosti ili s ruba trokuta 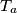 ,
, 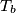 ,
, 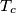 su redom nožišta okomica iz
su redom nožišta okomica iz  ,
,  ,
, 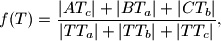 dokažite da
dokažite da 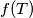 ne ovisi o izboru točke
ne ovisi o izboru točke  i
i  kutova
kutova 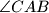 i
i  (
( ). Nađite kut
). Nađite kut 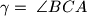 ako je
ako je 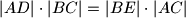 i
i 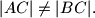
 ,
,  i
i  , pri čemu je
, pri čemu je 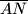 visina,
visina, 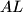 simetrala kuta
simetrala kuta 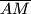 težišnica. Ako je
težišnica. Ako je 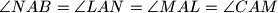 , odredite kutove trokuta.
, odredite kutove trokuta.