Zadana je hiperbola sa središtem  . Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama
. Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama  i
i  tako da je
tako da je 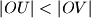 . Neka je točka
. Neka je točka  presjek okomice na realnu os hiperbole u točki
presjek okomice na realnu os hiperbole u točki  i polukružnice s promjerom
i polukružnice s promjerom 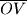 . Dokaži da je
. Dokaži da je 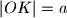 , pri čemu je
, pri čemu je  duljina realne poluosi dane hiperbole.
duljina realne poluosi dane hiperbole.
 . Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama
. Pravci kroz neku njenu točku paralelni njenim asimptotama sijeku realnu os te hiperbole u točkama  i
i  tako da je
tako da je 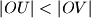 . Neka je točka
. Neka je točka  presjek okomice na realnu os hiperbole u točki
presjek okomice na realnu os hiperbole u točki  i polukružnice s promjerom
i polukružnice s promjerom 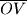 . Dokaži da je
. Dokaži da je 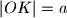 , pri čemu je
, pri čemu je  duljina realne poluosi dane hiperbole.
duljina realne poluosi dane hiperbole.  Školjka
Školjka