Neka je
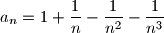
, gdje je
prirodan broj. Odredi najmanji prirodan broj
takav da je
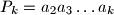
veći od
.
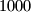
%V0
Neka je $ a_n=1+\dfrac1{n}-\dfrac1{n^2}-\dfrac1{n^3}$, gdje je $n$ prirodan broj. Odredi najmanji prirodan broj $k$ takav da je $$
P_k=a_2a_3\dots a_k
$$ veći od $1000$.
Školjka