Nazovimo prirodan broj

"sretan" ako mu je zbroj svih znamenaka višekratnik od

, i "supersretan" ako je "sretan" i niti jedan od brojeva
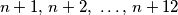
nije "sretan". Koji je najmanji "supersretan" prirodan broj?
%V0
Nazovimo prirodan broj $n$ "sretan" ako mu je zbroj svih znamenaka višekratnik od $7$, i "supersretan" ako je "sretan" i niti jedan od brojeva $$n + 1 \text{, } n + 2 \text{, } \ldots \text{, } n + 12$$ nije "sretan". Koji je najmanji "supersretan" prirodan broj?