Nađite sve parove realnih brojeva
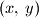
za koje vrijede jednakosti
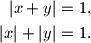
Prikažite skup rješenja u koordinatnoj ravnini.
%V0
Nađite sve parove realnih brojeva $(x,\,y)$ za koje vrijede jednakosti $$$\begin{align*}
|x+y|&=1\text{,} \\
|x|+|y|&=1\text{.}
\end{align*}
$$$ Prikažite skup rješenja u koordinatnoj ravnini.