Pravokutni trokut

s katetama duljina

cm i

cm i pravim kutom u vrhu

sukladan je trokutu
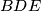
s pravim kutom u vrhu

. Točka

leži unutar dužine

, a točke

i

nalaze se s iste strane pravca

.
a) Odredi udaljenost točaka

i

.
b) Izračunaj površinu presjeka trokuta

i
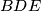
.
%V0
Pravokutni trokut $ABC$ s katetama duljina $15$ cm i $20$ cm i pravim kutom u vrhu $B$ sukladan je trokutu $BDE$ s pravim kutom u vrhu $D$. Točka $C$ leži unutar dužine $\overline{BD}$, a točke $A$ i $E$ nalaze se s iste strane pravca $BD$.
a) Odredi udaljenost točaka $A$ i $E$.
b) Izračunaj površinu presjeka trokuta $ABC$ i $BDE$.