Iz neke točke hipotenuze pravokutnog trokuta spuste se okomice na katete. Neka su nožišta tih okomica
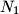
i
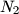
. Kada će spojnica tih nožišta,
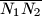
, biti najkraća? Kolika je duljina te najkraće spojnice ako su duljine kateta

i

?
%V0
Iz neke točke hipotenuze pravokutnog trokuta spuste se okomice na katete. Neka su nožišta tih okomica $N_1$ i $N_2$. Kada će spojnica tih nožišta, $\overline{N_1 N_2}$, biti najkraća? Kolika je duljina te najkraće spojnice ako su duljine kateta $a$ i $b$?