Slični zadaci
Stranica  trokuta
trokuta  dira njegovu upisanu kružnicu u točki
dira njegovu upisanu kružnicu u točki  , a tom trokutu pripisana kružnica uz stranicu
, a tom trokutu pripisana kružnica uz stranicu  dira tu stranicu u točki
dira tu stranicu u točki  . Dokaži da su točke
. Dokaži da su točke  i
i  simetrične u odnosu na polovište stranice
simetrične u odnosu na polovište stranice  .
.
(Trokutu pripisana kružnica je kružnica koja dodiruje jednu stranicu trokuta i produžetke drugih dviju stranica.)
 trokuta
trokuta  dira njegovu upisanu kružnicu u točki
dira njegovu upisanu kružnicu u točki  , a tom trokutu pripisana kružnica uz stranicu
, a tom trokutu pripisana kružnica uz stranicu  dira tu stranicu u točki
dira tu stranicu u točki  . Dokaži da su točke
. Dokaži da su točke  i
i  simetrične u odnosu na polovište stranice
simetrične u odnosu na polovište stranice  .
.(Trokutu pripisana kružnica je kružnica koja dodiruje jednu stranicu trokuta i produžetke drugih dviju stranica.)
 Školjka
Školjka 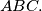 Neka je
Neka je 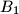 točka na visini tog trokuta povučenoj iz vrha
točka na visini tog trokuta povučenoj iz vrha  takva da je
takva da je 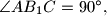 a
a 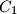 točka na visini tog trokuta povučenoj iz vrha
točka na visini tog trokuta povučenoj iz vrha  takva da je
takva da je 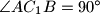 . Dokažite da je
. Dokažite da je 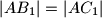 .
. 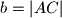 i
i 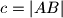 i
i 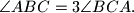 Na stranici
Na stranici  odabrane su točke
odabrane su točke 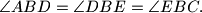 Izrazite pomoću
Izrazite pomoću  i
i  duljine dužina
duljine dužina 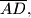
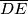 i
i 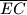 .
. 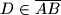 i
i 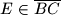 takve da je
takve da je 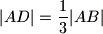 i
i 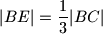 . Pravci
. Pravci  i
i  sijeku se u točki
sijeku se u točki  . Koliki je kut
. Koliki je kut 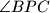 ?
? 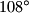 . Dokažite da je omjer duljina osnovice i kraka tog trokuta jednak
. Dokažite da je omjer duljina osnovice i kraka tog trokuta jednak 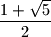 .
.  cm, a duljina težišnice iz vrha pravog kuta
cm, a duljina težišnice iz vrha pravog kuta  cm. Odredi zbroj duljina kateta tog trokuta.
cm. Odredi zbroj duljina kateta tog trokuta. 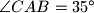 i
i 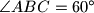 . Ako je
. Ako je  tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu
tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu  paralela s pravcem
paralela s pravcem  kroz vrh
kroz vrh