U trokutu

poznati su kutovi
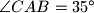
i
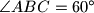
. Ako je

tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu

, a

paralela s pravcem

kroz vrh

, odredi kut između pravaca

i

.
%V0
U trokutu $ABC$ poznati su kutovi $\angle CAB=35^\circ$ i $\angle ABC=60^\circ$. Ako je $t$ tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu $C$, a $p$ paralela s pravcem $AB$ kroz vrh $C$, odredi kut između pravaca $p$ i $t$.