Dani su kompleksni brojevi
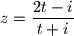
za
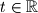
.

Koje sve vrijednosti može poprimiti
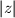
?

Odredite skup parametara

za koje vrijedi
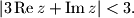
%V0
Dani su kompleksni brojevi $z=\dfrac{2t-i}{t+i}$ za $t \in \mathbb{R}$.
$a)$ Koje sve vrijednosti može poprimiti $|z|$?
$b)$ Odredite skup parametara $t$ za koje vrijedi $$| 3 \, \mbox{Re} \, z + \mbox{Im} \, z| < 3 \text{.}$$