Neka je

paralelogram,

polovište stranice

,

polovište stranice

i

sjecište dužina
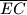
i
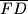
. Dokaži da dužine
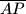
,
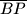
,
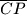
i
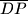
dijele paralelogram na trokute čije se površine u nekom poretku odnose kao
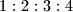
.
%V0
Neka je $ABCD$ paralelogram, $E$ polovište stranice $\overline{AB}$, $F$ polovište stranice $\overline{BC}$ i $P$ sjecište dužina $\overline{EC}$ i $\overline{FD}$. Dokaži da dužine $\overline{AP}$, $\overline{BP}$, $\overline{CP}$ i $\overline{DP}$ dijele paralelogram na trokute čije se površine u nekom poretku odnose kao $1:2:3:4$.