Duljine osnovica trapeza su

i

(
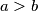
), a visina

. Njegove dijagonale su međusobno okomite, a kut između krakova je

. Dokažite da vrijedi
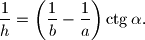
%V0
Duljine osnovica trapeza su $a$ i $b$ ($a > b$), a visina $h$. Njegove dijagonale su međusobno okomite, a kut između krakova je $\alpha $. Dokažite da vrijedi $$
\frac{1}{h} = \left(\frac{1}{b} - \frac{1}{a}\right)\ctg \alpha.
$$