Kamp '13 - Angle Chasing
Neka je  zajednička tetiva dviju kružnica. Pravac kroz
zajednička tetiva dviju kružnica. Pravac kroz  siječe jednu kružnicu u
siječe jednu kružnicu u  , a drugu u
, a drugu u  . Tangente u točkama
. Tangente u točkama  i
i  sijeku se u točki
sijeku se u točki  . Dokažite da je četverokut
. Dokažite da je četverokut 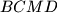 tetivan. (hint: Prvo dokažite da je kut između tetive nad lukom kružnice i tangente u jednom od krajeva tetive jednak obodnom kutu nad tim lukom.)
tetivan. (hint: Prvo dokažite da je kut između tetive nad lukom kružnice i tangente u jednom od krajeva tetive jednak obodnom kutu nad tim lukom.)
 zajednička tetiva dviju kružnica. Pravac kroz
zajednička tetiva dviju kružnica. Pravac kroz  siječe jednu kružnicu u
siječe jednu kružnicu u  , a drugu u
, a drugu u  . Tangente u točkama
. Tangente u točkama  i
i  sijeku se u točki
sijeku se u točki  . Dokažite da je četverokut
. Dokažite da je četverokut 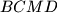 tetivan. (hint: Prvo dokažite da je kut između tetive nad lukom kružnice i tangente u jednom od krajeva tetive jednak obodnom kutu nad tim lukom.)
tetivan. (hint: Prvo dokažite da je kut između tetive nad lukom kružnice i tangente u jednom od krajeva tetive jednak obodnom kutu nad tim lukom.)  Školjka
Školjka  nalaze redom na stranicama
nalaze redom na stranicama  trokuta
trokuta  . Simetrale kutova
. Simetrale kutova 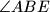 i
i 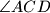 sijeku se u točki
sijeku se u točki  . Dokažite da je
. Dokažite da je 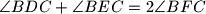 .
.  i
i  kvadrata
kvadrata  konstruirani su jednakostranični trokuti
konstruirani su jednakostranični trokuti 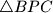 i
i 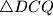 . Dokažite da je trokut
. Dokažite da je trokut 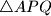 jednakostraničan.
jednakostraničan.  i
i  su redom središta opisane i upisane kružnice trokuta. Izrazite
su redom središta opisane i upisane kružnice trokuta. Izrazite 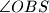 pomoću kuteva
pomoću kuteva  ,
,  i
i  .
.  pravokutan trokut s pravim kutom pri vrhu
pravokutan trokut s pravim kutom pri vrhu 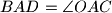 .
.  opisana trokutu
opisana trokutu 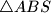 siječe pravac
siječe pravac  opisana trokutu
opisana trokutu 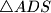 siječe pravac
siječe pravac  . Dokažite da su točke
. Dokažite da su točke  međusobno okomite. Neka je
međusobno okomite. Neka je  na stranicu
na stranicu  . Dokažite da vrijedi
. Dokažite da vrijedi 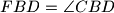 .
.  ,
,  tako da je
tako da je 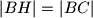 ,
, 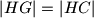 ,
, 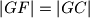 ,
, 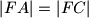 te
te 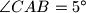 . Izračunajte koliki je
. Izračunajte koliki je  .
. 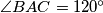 . Točka
. Točka 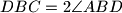 i
i 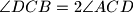 . Izračunaj mjeru kuta
. Izračunaj mjeru kuta 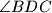 .
. 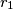 i
i 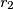 (
(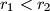 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  jedna tangenta na
jedna tangenta na  i paralelna je zajedničkom promjeru danih kružnica. Neka su
i paralelna je zajedničkom promjeru danih kružnica. Neka su 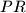 simetrala kuta
simetrala kuta 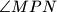 .
.  upisane kružnice trokuta
upisane kružnice trokuta 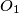 ,
, 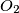 ,
, 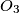 središta kružnica opisanih trokutima
središta kružnica opisanih trokutima 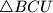 ,
, 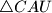 ,
, 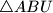 . Dokažite da kružnice opisane trokutima
. Dokažite da kružnice opisane trokutima 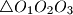 imaju zajedničko središte.
imaju zajedničko središte.  i simetrale kuta
i simetrale kuta 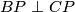 .
. 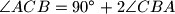 , a
, a 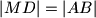 .
.  -terokuta jednak
-terokuta jednak 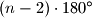 .
. 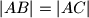 i
i 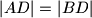 . Ako je za kutove
. Ako je za kutove 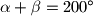 , odredite kut
, odredite kut 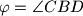 .
.