Ćevidova lema. Neka se dvije kružnice

,

sijeku u točkama

,

. Neka su na

odabrane dvije točke

,

. Neka tangenta iz

dira

u

, tangenta iz

dira

u

, tangenta iz

dira

u

, te tangenta iz

dira

u

. Također, neka su sve tangente s iste strane pravca

. Dokaži da je
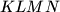
tetivan.
%V0
Ćevidova lema. Neka se dvije kružnice $k_1$, $k_2$ sijeku u točkama $A$, $B$. Neka su na $AB$ odabrane dvije točke $X$, $Y$. Neka tangenta iz $X$ dira $k_1$ u $K$, tangenta iz $X$ dira $k_2$ u $L$, tangenta iz $Y$ dira $k_1$ u $M$, te tangenta iz $Y$ dira $k_2$ u $N$. Također, neka su sve tangente s iste strane pravca $AB$. Dokaži da je $KLMN$ tetivan.