Simulacija općinskog 2016
Svaki od  kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
 kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.
kuhara zna dio nekog recepta za kolač (i svi znaju različite dijelove recepta, a zajedno znaju čitav recept). Dopušteno im je razmjenjivanje svih informacija koje znaju preko telefona, ali tako da u jednom telefonskom razgovoru sudjeluju točno dva kuhara i tijekom tog razgovora točno jedan od njih govori. Odredite najmanji broj telefonskih poziva potrebnih da bi svi kuhari znali čitav recept.  Školjka
Školjka 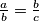 , gdje su
, gdje su  realni brojevi različiti od nule. Dokažite da tada vrijedi:
realni brojevi različiti od nule. Dokažite da tada vrijedi: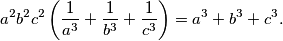
 simetrala kuta
simetrala kuta 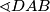 raspolavlja dužinu
raspolavlja dužinu  . Ako sa
. Ako sa  označimo polovište dužine
označimo polovište dužine 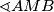 .
. 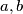 ,
, 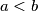 , takve da za sve realne brojeve
, takve da za sve realne brojeve ![x,y\in[a,b]](/media/m/1/0/e/10eecd0a7becb8f46e40e628617729df.png) vrijedi
vrijedi![\frac{1}{x}+\frac{1}{y}\in[a,b].](/media/m/c/3/1/c311e45b444da431a5bca5874bb927ef.png)
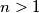 koji je barem 2016 puta veći od svakog od svojih prostih faktora,
koji je barem 2016 puta veći od svakog od svojih prostih faktora,