Simulacija županijskog 2016
Za okruglim stolom sjedi 10 učenika. Svaki od učenika zamisli jedan realan broj i taj broj priopći samo svojim susjedima (učenicima koji sjede lijevo i desno od njega) tako da ga pritom drugi učenici ne čuju. Nakon toga, idući u krug, svaki učenik javno kaže aritmetičku sredinu dva broja koja je saznao od svojih susjeda. Ako su redom izrečeni brojevi 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, koji je broj zamislio učenik koji je javno rekao broj 6?
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
Napomena. Aritmetička sredina dva realna broja jest jednaka zbroju tih brojeva podijeljenim s 2.
 Školjka
Školjka  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 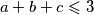 . Odredite najmanju moguću vrijednost izraza
. Odredite najmanju moguću vrijednost izraza 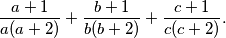
 takve da za četiri najmanja djelitelja
takve da za četiri najmanja djelitelja 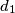 ,
, 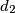 ,
, 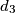 ,
, 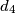 od
od 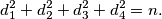
 dira stranicu
dira stranicu  u točki
u točki  . Neka su točke
. Neka su točke  i
i  , tim redom, na stranicama
, tim redom, na stranicama  i
i  takve da su pravci
takve da su pravci  i
i  paralelni te da je pravac
paralelni te da je pravac  diralište upisane kružnice i pravca
diralište upisane kružnice i pravca  sjecište pravaca
sjecište pravaca  i
i 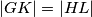 .
. 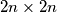 upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem
upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem 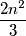 puta.
puta.