2. teža simulacija državnog natjecanja 2020.
Neka je  prirodan broj veći od
prirodan broj veći od  . Na kružnici je
. Na kružnici je 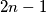 jednako udaljenih točaka od kojih je točno
jednako udaljenih točaka od kojih je točno  obojano crveno. Takvo bojanje zovemo
obojano crveno. Takvo bojanje zovemo 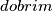 ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno
ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno  točaka. Odredi najmanji mogući
točaka. Odredi najmanji mogući  za koji je svako bojanje točaka na kružnici
za koji je svako bojanje točaka na kružnici 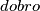 .
.
 Školjka
Školjka 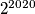 sa svojstvom da kada umnošku bilo koja
sa svojstvom da kada umnošku bilo koja  ta broja dodamo
ta broja dodamo  dobijemo potpuni kvadrat?
dobijemo potpuni kvadrat?  polinom sa realnim koeficijentima stupnja
polinom sa realnim koeficijentima stupnja 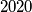 . Ako
. Ako 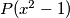 ima
ima 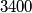 realnih nultočaka, a
realnih nultočaka, a 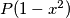 ima
ima 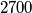 realnih nultočaka, dokaži da onda postoje dvije realne nultočke od
realnih nultočaka, dokaži da onda postoje dvije realne nultočke od 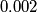 .
.  i
i  za koje vrijedi da je
za koje vrijedi da je 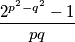 umnožak točno
umnožak točno  i
i 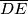 kružnice
kružnice  sijeku se u
sijeku se u  . Pravac kroz
. Pravac kroz  paralelan sa
paralelan sa  , a
, a 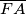 siječe
siječe  . Neka je
. Neka je  presjek
presjek 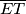 i
i  preslika
preslika 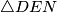 .
.