Kombinatorika mix (Napredna grupa)
Iza sedam brda i sedam mora, sedam planina i sedam dolina, sedam rijeka i sedam jezera, sedam sela i sedam šuma, negdje iza sedam Kaštela, sedam patuljaka čuva blago sakriveno iza sedam vrata, a svaka vrata čuva po sedam brava. Svaki patuljak ima neki broj ključeva, a svaki ključ otvara točno jednu bravu. Ako bilo koja tri patuljka mogu otvoriti svih sedam vrata i time doći do blaga, pokaži da patuljci zajedno imaju barem 245 ključeva.
Matej ima zlatnu šipku mase 2022 gram. Odlučio je odsjesti u hotelu koji će mu naplaćivati jedan gram zlata po noćenju, što Matej mora platiti svakoga jutra. Na početku u hotelu nema zlata, no kako će Matej plaćati će hotel također dobiti neku količinu zlata koju će moći koristiti za izvraćanje. Zato Matej može na nekim šipki učiniti rezove, čime bi stvorio dvije manje šipke. Ako Matej želi u hotelu odsjesti svih 2022 dana, na koliko najmanje manjih šipki mora izrezati početnu šipku da bi mogao svakoga dana platiti točno jedan gram (uz mogućnost izvraćanja viška od hotela, ukoliko hotel posjeduje šipke kojima može izvratiti točnu količinu)?
Matej ima zlatni lanac duljine 2022 karike (svake dvije susjedne karike su provučene jedna kroz drugu, osim onih krajnjih). Odlučio je odsjesti u hotelu koji će mu naplaćivati jednu zlatnu kariku po noćenju, što Matej mora platiti svakoga jutra. Na početku u hotelu nema zlata, no kako će Matej plaćati će hotel također dobiti neku količinu zlata koju će moći koristiti za izvraćanje. Zato Matej može na nekim karikama učiniti rezove, čime bi stvorio dva manja lanca i oslobodio tu kariku iz oba. Ako Matej želi u hotelu odsjesti svih 2022 dana, na koliko najmanje karika mora izrezati da bi mogao svakoga dana platiti točno jednu kariku (uz mogućnost izvraćanja viška od hotela ukoliko hotel posjeduje lance kojima može izvratiti točnu količinu)?
Na stol je postavljeno 2022 karte pri čemu su sve okrenute na zlatnu stranu, a plava strana je na stolu. Matej i Emanuel igraju sljedeću igru: igrač koji je na potezu bira neku kartu koja trenutno pokazuje zlatnu stranu i okreće nju i 49 karata njoj s lijeva na drugu stranu (one koje su pokazivale zlatnu stranu sad pokazuju plavu, a one koje su pokazivale plavu stranu sad pokazuju zlatnu). Pobjednik je onaj koji odigra zadnji potez. Ako Matej ide prvi, tko će pobijediti?
 Školjka
Školjka 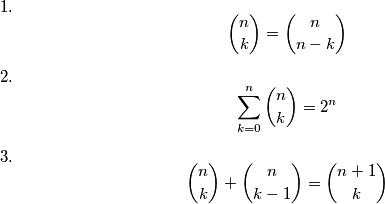
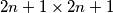 , s time da se zemlja nalazi u poljima koja su presjek redova i stupaca parnih rednih oznaka, a na ostalim mjestima se nalazi pod. Za koje vrijednosti
, s time da se zemlja nalazi u poljima koja su presjek redova i stupaca parnih rednih oznaka, a na ostalim mjestima se nalazi pod. Za koje vrijednosti  Nika može popločati svoj vrt dominama?
Nika može popločati svoj vrt dominama? 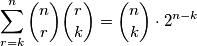
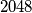 tenisača i svaki je odigrao protiv svakog drugog barem jednom i meč je završio nečijom pobjedom. Pokaži da je moguće pronaći
tenisača i svaki je odigrao protiv svakog drugog barem jednom i meč je završio nečijom pobjedom. Pokaži da je moguće pronaći  igrača tako da je prvi od njih pobjedio sve ostale, drugi sve osim prvog, treći sve osim prva dva...
igrača tako da je prvi od njih pobjedio sve ostale, drugi sve osim prvog, treći sve osim prva dva... 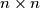 ploča čija su polja obojena u
ploča čija su polja obojena u 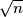 različitih boja.
različitih boja.  dijelova i particija kojima je najveći dio točno
dijelova i particija kojima je najveći dio točno