Neka su

,

,

,

članovi aritmetičkog i
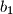
,
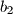
,

,
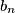
članovi geometrijskog niza s pozitivnim članovima. Ako je
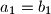
i
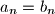
, dokažite da je suma članova aritmetičkog niza veća ili jednaka od sume članova geometrijskog niza.
%V0
Neka su $a_1$, $a_2$, $\dots$, $a_n$ članovi aritmetičkog i $b_1$, $b_2$, $\dots$, $b_n$ članovi geometrijskog niza s pozitivnim članovima. Ako je $a_1=b_1$ i $a_n=b_n$, dokažite da je suma članova aritmetičkog niza veća ili jednaka od sume članova geometrijskog niza.