Na stranici

trokuta

odabrana je bilo koja točka

, a na stranici

točka

, tako da je

paralelno s

. Neka su

,
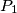
i
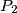
redom površine trokuta

,
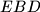
i

, dokaži da je tada
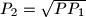
.
%V0
Na stranici $\overline{BC}$ trokuta $ABC$ odabrana je bilo koja točka $D$, a na stranici $\overline{AB}$ točka $E$, tako da je $DE$ paralelno s $CA$. Neka su $P$, $P_1$ i $P_2$ redom površine trokuta $ABC$, $EBD$ i $ABD$, dokaži da je tada $P_2=\sqrt{PP_1}$.