Slični zadaci
Prvi član aritmetičkog niza 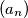 , kojem su svi članovi prirodni brojevi, je
, kojem su svi članovi prirodni brojevi, je 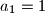 . Broj
. Broj 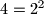 jest, a
jest, a  nije član tog niza.
nije član tog niza.
 Dokažite da postoji jedan i samo jedan takav niz. Napišite njegov opći član.
Dokažite da postoji jedan i samo jedan takav niz. Napišite njegov opći član.
 Pokažite da je kvadrat svakog prirodnog broja, koji nije djeljiv s
Pokažite da je kvadrat svakog prirodnog broja, koji nije djeljiv s  , član tog niza.
, član tog niza.
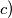 Provjerite da su brojevi
Provjerite da su brojevi 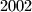 i
i 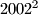 članovi tog niza. Odredite njihove indekse.
članovi tog niza. Odredite njihove indekse.
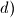 Obrazložite zaključak: kvadrat svakog člana niza je član niza. Vrijedi li obrat, tj. ako je kvadrat nekog broja član tog niza, onda je i taj broj član niza.
Obrazložite zaključak: kvadrat svakog člana niza je član niza. Vrijedi li obrat, tj. ako je kvadrat nekog broja član tog niza, onda je i taj broj član niza.
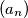 , kojem su svi članovi prirodni brojevi, je
, kojem su svi članovi prirodni brojevi, je 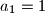 . Broj
. Broj 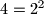 jest, a
jest, a  nije član tog niza.
nije član tog niza. Dokažite da postoji jedan i samo jedan takav niz. Napišite njegov opći član.
Dokažite da postoji jedan i samo jedan takav niz. Napišite njegov opći član. Pokažite da je kvadrat svakog prirodnog broja, koji nije djeljiv s
Pokažite da je kvadrat svakog prirodnog broja, koji nije djeljiv s  , član tog niza.
, član tog niza.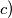 Provjerite da su brojevi
Provjerite da su brojevi 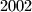 i
i 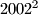 članovi tog niza. Odredite njihove indekse.
članovi tog niza. Odredite njihove indekse.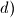 Obrazložite zaključak: kvadrat svakog člana niza je član niza. Vrijedi li obrat, tj. ako je kvadrat nekog broja član tog niza, onda je i taj broj član niza.
Obrazložite zaključak: kvadrat svakog člana niza je član niza. Vrijedi li obrat, tj. ako je kvadrat nekog broja član tog niza, onda je i taj broj član niza.  Školjka
Školjka 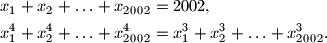
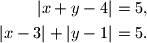
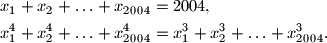
 ,
,  za koje vrijedi
za koje vrijedi 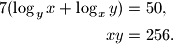
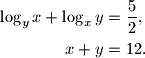
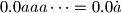 . Koje vrijednosti može poprimiti znamenka
. Koje vrijednosti može poprimiti znamenka  ?
?