Neka je
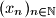
niz realnih brojeva različitih od nule takav da vrijedi
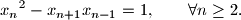
Dokaži da izraz
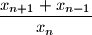
poprima istu vrijednost za svaki
.
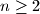
%V0
Neka je $(x_n)_{n \in \mathbb{N} }$ niz realnih brojeva različitih od nule takav da vrijedi $$
{x_n}^2-x_{n+1}x_{n-1}=1,\qquad \forall n\geq 2.
$$
Dokaži da izraz $\dfrac{x_{n+1}+x_{n-1}}{x_n}$ poprima istu vrijednost za svaki $n\geq 2$.
Školjka