Na krakovima šiljastog kuta

s vrhom

dane su točke

i

, tako da je
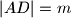
i
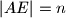
. U točkama

i

povučene su okomice na krakove kuta na kojima leže. Ako se te dvije okomice sijeku u točki

u unutrašnjosti kuta, dokažite da je
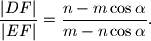
%V0
Na krakovima šiljastog kuta $\alpha $ s vrhom $A$ dane su točke $D$ i $E$, tako da je $|AD|=m$ i $|AE|=n$. U točkama $D$ i $E$ povučene su okomice na krakove kuta na kojima leže. Ako se te dvije okomice sijeku u točki $F$ u unutrašnjosti kuta, dokažite da je $$
\frac{|DF|}{|EF|}=\frac{n-m\cos \alpha }{m-n\cos \alpha }.
$$