Može li se ploča
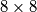
bez kutnih polja prekriti s

pločica oblika

ili

?
%V0
Može li se ploča $8 \times 8$ bez kutnih polja prekriti s $15$ pločica oblika $\setlength{\unitlength}{5pt} \begin{picture}(3, 2) \put(0, 0){\line(1, 0){3}} \put(0, 0){\line(0, 1){2}} \put(3, 1){\line(-1, 0){3}} \put(3, 1){\line(0, -1){1}} \put(1, 0){\line(0, 1){2}} \put(0, 2){\line(1, 0){1}} \put(2, 0){\line(0, 1){1}} \end{picture}$ ili $\setlength{\unitlength}{5pt} \begin{picture}(3, 2) \put(0, 0){\line(1, 0){1}} \put(0, 0){\line(0, 1){2}} \put(3, 2){\line(-1, 0){3}} \put(3, 2){\line(0, -1){1}} \put(1, 0){\line(0, 1){2}} \put(0, 1){\line(1, 0){3}} \put(2, 2){\line(0, -1){1}} \end{picture}$?