Slični zadaci
A soldier needs to check if there are any mines in the interior or on the sides of an equilateral triangle  His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
 His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?  Školjka
Školjka  such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.
such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.  we have
we have 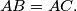 A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides
A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides 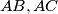 in the points
in the points 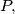 respectively
respectively 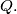 Prove that the midpoint of
Prove that the midpoint of  is the center of the inscribed circle of the triangle
is the center of the inscribed circle of the triangle 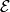 the set of all points contained in the three segments
the set of all points contained in the three segments  ,
,  , and
, and  (including
(including  ,
,  , and
, and  ). Determine whether, for every partition of
). Determine whether, for every partition of 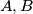 be adjacent vertices of a regular
be adjacent vertices of a regular  -gon (
-gon (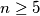 ) with center
) with center  . A triangle
. A triangle 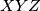 , which is congruent to and initially coincides with
, which is congruent to and initially coincides with 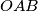 , moves in the plane in such a way that
, moves in the plane in such a way that  and
and  each trace out the whole boundary of the polygon, with
each trace out the whole boundary of the polygon, with  remaining inside the polygon. Find the locus of
remaining inside the polygon. Find the locus of 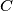 be a circle,
be a circle, 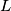 a line tangent to the circle
a line tangent to the circle 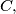 and
and 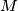 a point on
a point on 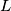 . Find the locus of all points
. Find the locus of all points 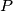 with the following property: there exists two points
with the following property: there exists two points 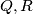 on
on 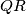 and
and 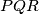 .
.