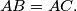
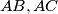
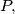
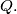
In a triangle we have A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides in the points respectively Prove that the midpoint of is the center of the inscribed circle of the triangle
%V0
In a triangle $ABC$ we have $AB = AC.$ A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides $AB, AC$ in the points $P,$ respectively $Q.$ Prove that the midpoint of $PQ$ is the center of the inscribed circle of the triangle $ABC.$
Izvor: Međunarodna matematička olimpijada, shortlist 1978
Školjka 
we have 
A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides 
in the points 
respectively 
Prove that the midpoint of 
is the center of the inscribed circle of the triangle 