Three disks of diameter  are touching a sphere in their centers. Besides, every disk touches the other two disks. How to choose the radius
are touching a sphere in their centers. Besides, every disk touches the other two disks. How to choose the radius 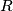 of the sphere in order that axis of the whole figure has an angle of
of the sphere in order that axis of the whole figure has an angle of 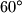 with the line connecting the center of the sphere with the point of the disks which is at the largest distance from the axis ? (The axis of the figure is the line having the property that rotation of the figure of
with the line connecting the center of the sphere with the point of the disks which is at the largest distance from the axis ? (The axis of the figure is the line having the property that rotation of the figure of 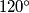 around that line brings the figure in the initial position. Disks are all on one side of the plane, passing through the center of the sphere and orthogonal to the axis).
around that line brings the figure in the initial position. Disks are all on one side of the plane, passing through the center of the sphere and orthogonal to the axis).
 are touching a sphere in their centers. Besides, every disk touches the other two disks. How to choose the radius
are touching a sphere in their centers. Besides, every disk touches the other two disks. How to choose the radius 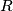 of the sphere in order that axis of the whole figure has an angle of
of the sphere in order that axis of the whole figure has an angle of 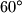 with the line connecting the center of the sphere with the point of the disks which is at the largest distance from the axis ? (The axis of the figure is the line having the property that rotation of the figure of
with the line connecting the center of the sphere with the point of the disks which is at the largest distance from the axis ? (The axis of the figure is the line having the property that rotation of the figure of 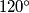 around that line brings the figure in the initial position. Disks are all on one side of the plane, passing through the center of the sphere and orthogonal to the axis).
around that line brings the figure in the initial position. Disks are all on one side of the plane, passing through the center of the sphere and orthogonal to the axis).  Školjka
Školjka