IMO Shortlist 1982 problem 18
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a point of three-dimensional space and let
be a point of three-dimensional space and let 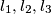 be mutually perpendicular straight lines passing through
be mutually perpendicular straight lines passing through  . Let
. Let  denote the sphere with center
denote the sphere with center  and radius
and radius  , and for every point
, and for every point  of
of  , let
, let 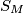 denote the sphere with center
denote the sphere with center  and radius
and radius  . We denote by
. We denote by 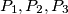 the intersection of
the intersection of 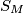 with the straight lines
with the straight lines 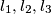 , respectively, where we put
, respectively, where we put 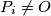 if
if 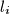 meets
meets 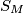 at two distinct points and
at two distinct points and 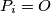 otherwise (
otherwise (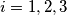 ). What is the set of centers of gravity of the (possibly degenerate) triangles
). What is the set of centers of gravity of the (possibly degenerate) triangles 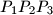 as
as  runs through the points of
runs through the points of  ?
?
 be a point of three-dimensional space and let
be a point of three-dimensional space and let 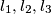 be mutually perpendicular straight lines passing through
be mutually perpendicular straight lines passing through  . Let
. Let  denote the sphere with center
denote the sphere with center  and radius
and radius  , and for every point
, and for every point  of
of  , let
, let 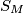 denote the sphere with center
denote the sphere with center  and radius
and radius  . We denote by
. We denote by 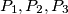 the intersection of
the intersection of 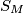 with the straight lines
with the straight lines 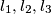 , respectively, where we put
, respectively, where we put 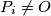 if
if 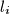 meets
meets 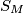 at two distinct points and
at two distinct points and 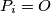 otherwise (
otherwise (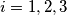 ). What is the set of centers of gravity of the (possibly degenerate) triangles
). What is the set of centers of gravity of the (possibly degenerate) triangles 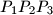 as
as  runs through the points of
runs through the points of  ?
? Izvor: Međunarodna matematička olimpijada, shortlist 1982
 Školjka
Školjka 
