Kružnica sa središtem
dira stranicu
i produžetke stranica
i
trokuta
redom u točkama
,
i
. Dužine
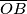
i
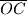
sijeku spojnicu
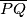
redom u točkama
i
. Dokažite da je
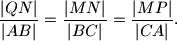
%V0
Kružnica sa središtem $O$ dira stranicu $\overline{BC}$ i produžetke stranica $\overline{AB}$ i $\overline{AC}$ trokuta $ABC$ redom u točkama $K$, $P$ i $Q$. Dužine $\overline{OB}$ i $\overline{OC}$ sijeku spojnicu $\overline{PQ}$ redom u točkama $M$ i $N$. Dokažite da je $$\frac{|QN|}{|AB|} = \frac{|MN|}{|BC|} = \frac{|MP|}{|CA|} \text{.}$$
Školjka