
is any point on the side

of the triangle

.
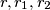
are the radii of the circles inscribed in
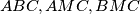
.
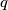
is the radius of the circle on the opposite side of

to

, touching the three sides of

and the extensions of

and
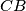
. Similarly,
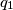
and
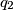
. Prove that
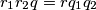
.
%V0
$M$ is any point on the side $AB$ of the triangle $ABC$. $r,r_1,r_2$ are the radii of the circles inscribed in $ABC,AMC,BMC$. $q$ is the radius of the circle on the opposite side of $AB$ to $C$, touching the three sides of $AB$ and the extensions of $CA$ and $CB$. Similarly, $q_1$ and $q_2$. Prove that $r_1r_2q=rq_1q_2$.