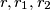
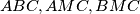
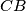
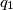
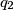
is any point on the side of the triangle . are the radii of the circles inscribed in . is the radius of the circle on the opposite side of to , touching the three sides of and the extensions of and . Similarly, and . Prove that .
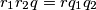
%V0
$M$ is any point on the side $AB$ of the triangle $ABC$. $r,r_1,r_2$ are the radii of the circles inscribed in $ABC,AMC,BMC$. $q$ is the radius of the circle on the opposite side of $AB$ to $C$, touching the three sides of $AB$ and the extensions of $CA$ and $CB$. Similarly, $q_1$ and $q_2$. Prove that $r_1r_2q=rq_1q_2$.
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
is any point on the side 
of the triangle 
. 
are the radii of the circles inscribed in 
. 
is the radius of the circle on the opposite side of 
, touching the three sides of 
and 
. Similarly, 
and 
. Prove that 
.