Neka je
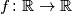
kvadratna funkcija
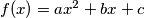
. Označimo sa

diskriminantu, sa

umnožak, a sa

zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija

za koju su

,

,

,

četiri uzastopna cijela broja (u rastućem poretku).
%V0
Neka je $f \colon \mathbb{R} \to \mathbb{R}$ kvadratna funkcija $f\!\left(x\right) = ax^2+bx+c$. Označimo sa $D$ diskriminantu, sa $P$ umnožak, a sa $S$ zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija $f$ za koju su $a$, $D$, $P$, $S$ četiri uzastopna cijela broja (u rastućem poretku).