Slični zadaci
Consider a plane  and three non-collinear points
and three non-collinear points  on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 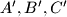 . Let
. Let 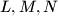 be the midpoints of segments
be the midpoints of segments 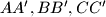 ; Let
; Let  be the centroid of the triangle
be the centroid of the triangle 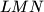 . (We will not consider positions of the points
. (We will not consider positions of the points 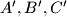 such that the points
such that the points 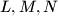 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point  as
as 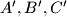 range independently over the plane
range independently over the plane  ?
?
 and three non-collinear points
and three non-collinear points  on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 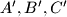 . Let
. Let 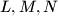 be the midpoints of segments
be the midpoints of segments 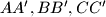 ; Let
; Let  be the centroid of the triangle
be the centroid of the triangle 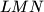 . (We will not consider positions of the points
. (We will not consider positions of the points 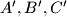 such that the points
such that the points 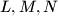 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point  as
as 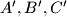 range independently over the plane
range independently over the plane  ?
? Let  be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 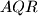 ,
, 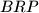 ,
, 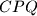 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
.
Alternative formulation: Let be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that
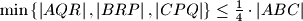 ,
,
where the abbreviation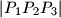 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 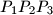 .
.
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 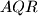 ,
, 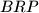 ,
, 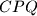 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
. Alternative formulation: Let
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that 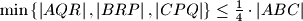 ,
, where the abbreviation
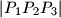 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 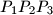 .
. Consider 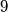 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
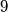 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.  Školjka
Školjka 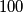 coplanar points, no three collinear, prove that at most
coplanar points, no three collinear, prove that at most 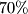 of the triangles formed by the points have all angles acute.
of the triangles formed by the points have all angles acute.  such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.
such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.  ,
,  and
and 
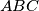 be a triangle and
be a triangle and 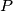 an interior point of
an interior point of 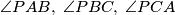 is less than or equal to
is less than or equal to 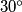 .
.