Slični zadaci
Let  be a natural number. Find a way to assign natural numbers to the vertices of a regular
be a natural number. Find a way to assign natural numbers to the vertices of a regular  -gon such that the following conditions are satisfied:
-gon such that the following conditions are satisfied:
(1) only digits and
and  are used;
are used;
(2) each number consists of exactly digits;
digits;
(3) different numbers are assigned to different vertices;
(4) the numbers assigned to two neighboring vertices differ at exactly one digit.
 be a natural number. Find a way to assign natural numbers to the vertices of a regular
be a natural number. Find a way to assign natural numbers to the vertices of a regular  -gon such that the following conditions are satisfied:
-gon such that the following conditions are satisfied:(1) only digits
 and
and  are used;
are used;(2) each number consists of exactly
 digits;
digits;(3) different numbers are assigned to different vertices;
(4) the numbers assigned to two neighboring vertices differ at exactly one digit.
 Školjka
Školjka 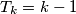 for
for 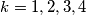 and
and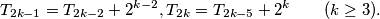
 ,
,![1 + T_{2n-1} = \left[ \frac{12}{7}2^{n-1} \right] \quad \text{and} \quad 1 + T_{2n} = \left[ \frac{17}{7}2^{n-1} \right],](/media/m/6/a/9/6a9da69111a0b8b7fb9e7d7f4579e3fe.png)
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png) denotes the greatest integer not exceeding
denotes the greatest integer not exceeding 
 (or
(or 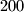 ) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer. 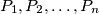 are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance 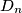 between any two of these points has its largest possible value
between any two of these points has its largest possible value 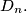 Calculate
Calculate 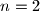 to 7. and justify your answer.
to 7. and justify your answer. 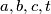 for which:
for which: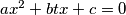 has two distinct real roots
has two distinct real roots 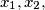
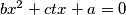 has two distinct real roots
has two distinct real roots 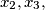
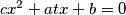 has two distinct real roots
has two distinct real roots 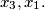
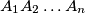 is drawn in a
is drawn in a 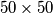 square, so that the distance from any point of the square to the broken line is less than
square, so that the distance from any point of the square to the broken line is less than 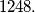
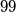 (not necessarily distinct) are written on
(not necessarily distinct) are written on