IMO Shortlist 1971 problem 15
Dodao/la:
arhiva2. travnja 2012. Natural numbers from
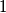
to
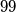
(not necessarily distinct) are written on
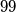
cards. It is given that the sum of the numbers on any subset of cards (including the set of all cards) is not divisible by
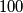
. Show that all the cards contain the same number.
%V0
Natural numbers from $1$ to $99$ (not necessarily distinct) are written on $99$ cards. It is given that the sum of the numbers on any subset of cards (including the set of all cards) is not divisible by $100$. Show that all the cards contain the same number.
Izvor: Međunarodna matematička olimpijada, shortlist 1971