A sphere

is tangent to the edges
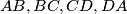
of a tetrahedron

at the points
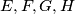
respectively. The points
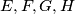
are the vertices of a square. Prove that if the sphere is tangent to the edge

, then it is also tangent to the edge
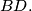
%V0
A sphere $S$ is tangent to the edges $AB,BC,CD,DA$ of a tetrahedron $ABCD$ at the points $E,F,G,H$ respectively. The points $E,F,G,H$ are the vertices of a square. Prove that if the sphere is tangent to the edge $AC$, then it is also tangent to the edge $BD.$