Consider the two square matrices
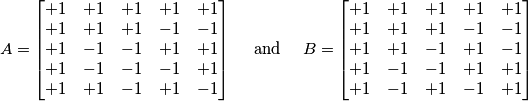
with entries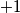 and
and 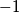 . The following operations will be called elementary:
. The following operations will be called elementary:
(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations.
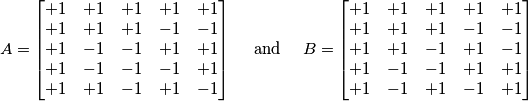
with entries
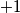 and
and 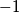 . The following operations will be called elementary:
. The following operations will be called elementary:(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix
 cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations. Slični zadaci
In town  there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 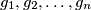 and
and 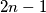 boys
boys 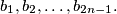 The girl
The girl 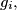
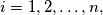 knows the boys
knows the boys 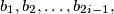 and no others. For all
and no others. For all 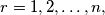 denote by
denote by 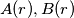 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 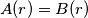 for each
for each 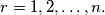
 there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 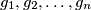 and
and 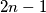 boys
boys 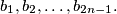 The girl
The girl 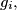
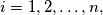 knows the boys
knows the boys 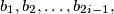 and no others. For all
and no others. For all 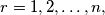 denote by
denote by 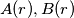 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 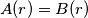 for each
for each 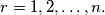
Initially, only the integer 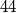 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 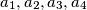 such that the arithmetic mean
such that the arithmetic mean 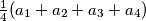 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 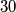 steps we end up with
steps we end up with 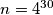 integers
integers 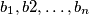 on the board. Prove that
on the board. Prove that 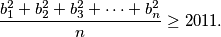
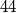 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 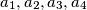 such that the arithmetic mean
such that the arithmetic mean 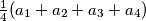 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 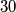 steps we end up with
steps we end up with 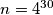 integers
integers 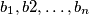 on the board. Prove that
on the board. Prove that 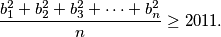
 Školjka
Školjka 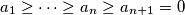 be real numbers. Show that
be real numbers. Show that 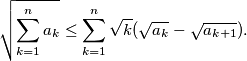
 determine the minimum value that the sum
determine the minimum value that the sum 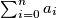 can take for nonnegative numbers
can take for nonnegative numbers 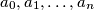 satisfying the condition
satisfying the condition 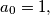
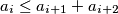 for
for 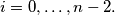
 podskup skupa
podskup skupa 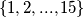 koji ne sadrži
koji ne sadrži  elementa čiji je umnožak potpun kvadrat. Odredi maksimalan broj elemenata skupa
elementa čiji je umnožak potpun kvadrat. Odredi maksimalan broj elemenata skupa  sastoji se od
sastoji se od 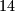 prirodnih brojeva. Pokažite da postoji
prirodnih brojeva. Pokažite da postoji 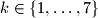 za koji je moguće naci
za koji je moguće naci  -člane disjunktne podskupove
-člane disjunktne podskupove  i
i  skupa
skupa 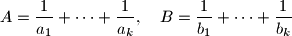 razlikuju za manje od
razlikuju za manje od 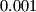 .
.